「台湾の論文によると無症状感染の確率は０．４％」はデマ

２０２０年５月１日の台湾の論文を引用して、

「厚労省がその根拠とする台湾の論文には、無症状感染の確率は０．４％であると書かれている。無症状感染者と濃厚接触しても感染しない確率は９９．６％以上だ」

と主張する人がいますが、デマです。

感染確率の調査を目的とした論文ではない

デマッターが根拠としている台湾の論文がこちらです。

「Contact Tracing Assessment of COVID-19 Transmission Dynamics in Taiwan and Risk at Different Exposure Periods Before and After Symptom Onset」

そもそも、この論文は、「無症状感染者の感染確率」の調査を目的とした論文ではありません。

この論文は、新型コロナ感染者の「発症前後の感染リスク」について調査したものであり、厚労省が根拠としているのもその点です。

Objective：To delineate the transmission dynamics of COVID-19 and evaluate the transmission risk at different exposure window periods before and after symptom onset.
目的：新型コロナの感染動態を明らかにし、症状の発症前後のさまざまな曝露期間での感染リスクを評価すること。

Conclusions
結論
In summary, the findings of this study suggest that most transmission of COVID-19 occurred at the very early stage of the disease or even before the onset of symptoms
要約すると、この研究結果は次のことを示唆しています。つまり、新型コロナのほとんどの感染が、病気の非常に初期の段階または症状の発症前でさえ起こるということ

つまり正確な感染確率を調べるための条件を揃えて行った調査ではなく、この論文に「感染確率」の数値と根拠を求めるのは誤りです。

分かりやすい解説

上記論文の分かりやすい（？）日本語解説記事（他サイト）。

SARS-CoV-2が感染力をもつ期間についての考察
COVID-19感染力は発症前から発症5日後まで持続（医療従事者のみ。要登録）

濃厚接触者の定義

たとえば、この論文の調査における濃厚接触者は次のように定義されています。

The definition of a close contact was a person who did not wear appropriate personal protection equipment (PPE) while having face-to-face contact with a confirmed case for more than 15 minutes during the investigation period.
濃厚接触者の定義は、調査期間中に個人用防護具（PPE）を着用せず患者（初発症例）と対面で１５分以上接触した者

For health care settings, medical staff, hospital workers, and other patients in the same setting were included; close contact was defined by contacting an index case within 2 m without appropriate PPE and without a minimal requirement of exposure time.
医療施設では、PPEを着用せず発端者と２メートル以内の距離で接触した者

無症状者の感染確率を調べることが目的ならば、無症状感染者に対して「マスクなしで１５分だけおしゃべりをした人」や「（医療施設では）一瞬でも２ｍ以内に近付いた人」を調査対象とするのは不適切ですよね？

無症状者の感染確率を調べることが目的ならば、無症状感染者と同居する家族や、毎日のようにオフィスで会う会社の同僚などを（一定期間後に）調査対象にすべきではありませんか？

そもそも無症状感染者の感染確率調査は困難

そもそも、無症状感染者は無症状であるがゆえに、誰が感染させ誰が感染したかを正確に調べることは非常に困難です。

無症状感染の確率を調べるために、健康な人を集めて感染実験をすることは人道上も許されません。つまり自然にデータが集まるまで待つ必要があります。

この論文の研究調査が行われたのは２０２０年１月１５日からの約２カ月間です。つまりまだ新型コロナについてほとんど何も分かっていない時期でした。仮に、無症状感染者の感染確率を調べようと思ったとしても、当時はそのためのデータが不足していたことは容易に想像できます。

感染した人のうち約4割が無症状の感染者からと推計（WHO）

２０２０年６月９日、WHOは、新型コロナに感染した人のうち約４０％が無症状感染者からの感染だという推計があることを明らかにしています。

一時、無症状感染者からの感染は「非常にまれだ」とした見解を示したが、誤解があったと釈明。
感染した人のうち約4割が無症状の感染者からうつされているとする推計も紹介した
https://www.nikkei.com/article/DGXMZO60181520Q0A610C2EAF000/

Some models developed by other scientists suggest as much as 40% of global transmission may be due to asymptomatic individuals
他の科学者によって示されたいくつかのモデルでは、世界の感染の40％が無症状感染者によるものであることが示唆されている
https://www.cnbc.com/2020/06/10/dr-anthony-fauci-says-whos-remark-on-asymptomatic-coronavirus-spread-was-not-correct.html

性行為による感染確率データ

少し話がずれますが、感染症状が出ている人が性行為を行うでしょうか？普通に考えて、性行為を行うとしたら、感染症状が出ていないときか気付いてないときだと考えられませんか？

あくまでも参考レベルですが、性行為による感染確率を調べたデータがあります。

それによると、性行為により新型コロナをパートナーに感染させた確率は４２．９％でした。デマッターの主張する数値よりも、この数値のほうが無症状者の感染確率データとして参考にする価値がありませんか（濃厚接触中の濃厚接触の例ですが）。

Clinical features and sexual transmission potential of SARS-CoV-2 infected female patients: a descriptive study in Wuhan, China

ちなみに、「０．４％」という数字はどこから？

この論文を根拠に「無症状者の感染確率は０．４％だ」と主張する人がいますが、その数字はどこから来たのでしょうか？

前述したように、そもそもこの論文に無症状者の感染確率を求めるのは間違いなのですが、「０．４％」を主張する人の主張がどこから来たのか説明します。

最初、私は、論文の以下の文から取ってきた数字だと思いました。

with an infection risk of 0.8% (95% CI, 0.5%-1.2%). The secondary clinical attack rate was 18 of 2761, or 0.7% (95% CI, 0.4%-1.0%)
感染リスクは0.8%（95% CI 0.5-1.2%）であった．二次発病率は0.7%（95% CI,0.4-1.0%）（18/2761例）であった

CIについて

CI（Confidence interval、信頼区間、しんらいくかん）とは、統計学で母集団の真の値（母平均等）が含まれることが、かなり確信 (confident) できる数値範囲のことである。例えば95%CIとは、繰り返し信頼区間を求めたときに95%の確率でこの範囲に真値が存在することを意味する。

https://ja.wikipedia.org/wiki/%E4%BF%A1%E9%A0%BC%E5%8C%BA%E9%96%93

ですが、そうではないということを、ツイッターの知り合いの方々から教えていただきました。

「０．４％」を主張する鍼治療の先生、高橋徳氏が、動画の中で「０．４％」の根拠を説明していたんですね。

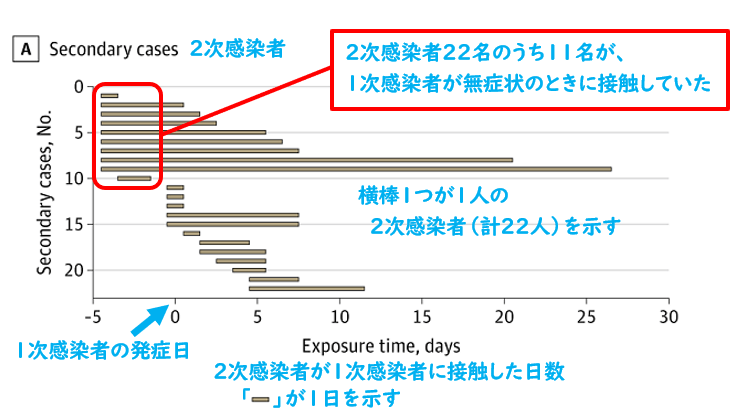
その説明によると、論文中の以下のグラフ（水色の字と赤い線はブログ主による）を根拠に、

１次感染者が無症状のときに、２次感染者のうち１１名が１次感染者と濃厚接触していた
だから、無症状感染率は、１１／［濃厚接触者総数２，７６１］×１００≒０．４％である

という主張でした。

論文中の関係する部分

Results
結果

We enrolled 100 confirmed patients, with a median age of 44 years (range, 11-88 years), including 44 men and 56 women.
（１次）感染者100人の患者が対象です。年齢の中央値が44歳（範囲は11〜88歳）で、男性44人と女性56人です。

Among their 2761 close contacts, there were 22 paired index-secondary cases.
100人の患者と濃厚接触した2,761人のうち、22人の２次感染者がありました。

The overall secondary clinical attack rate was 0.7% (95% CI, 0.4%-1.0%).
全体の２次発病率は0.7%（95% CI, 0.4%-1.0%）。

The attack rate was higher among the 1818 contacts whose exposure to index cases started within 5 days of symptom onset (1.0% [95% CI, 0.6%-1.6%]) compared with those who were exposed later (0 cases from 852 contacts; 95% CI, 0%-0.4%).
発病率は、発端者への曝露が症状の発症から5日以内に開始した1,818人の接触者（1.0％[95％ CI、0.6％-1.6％]）の方が、その後に曝露した人（852人の接触者から0例; 95％ CI、0％-0.4％）と比較して高かった。

The 299 contacts with exclusive presymptomatic exposures were also at risk (attack rate, 0.7% [95% CI, 0.2%-2.4%]).
（１次発症者が）発症前に１次感染者に接触した299人の接触者もリスクがあった（発病率、0.7％[95％ CI、0.2％-2.4％]）。

The attack rate was higher among household (4.6% [95% CI, 2.3%-9.3%]) and nonhousehold (5.3% [95% CI, 2.1%-12.8%]) family contacts than that in health care or other settings.
発病率は、医療または他の接触よりも、家庭内での接触（4.6％[95％CI、2.3％-9.3％]）および同居人の接触（5.3％[95％ CI、2.1％-12.8％]）のほうが高かった。

The attack rates were higher among those aged 40 to 59 years (1.1% [95% CI, 0.6%-2.1%]) and those aged 60 years and older (0.9% [95% CI, 0.3%-2.6%]).
発病率は40歳から59歳 (1.1% [95% CI, 0.6%-2.1%])と60歳以上 (0.9% [95% CI, 0.3%-2.6%])で高かった。

ちょっと待ってください。高橋徳氏の計算がおかしいことに気付きましたか？

無症状感染者の感染率を出したいならば、［無症状感染者に接触した人の総数］を分母にして、［その総数のうち感染した人数］を分子にする必要があります。そうですよね？

つまり、この場合の無症状感染率は、

１１／２９９×１００≒３．７％

となります（後述しますがこの解にはまだ問題があります）。

高橋徳氏は、無症状感染者に接触した人達だけでなく、有症状感染者に接触した人達も加え、濃厚接触者２，７６１人の全員を分母にしてしまっています。計算式を間違えているのでその答えである「０．４％」も間違いです。

ところで「この解にはまだ問題がある」と書いた点を説明します。実は論文には以下の記述があります。

None of the 9 asymptomatic case patients transmitted a secondary case.
無症状感染者のうち９人は、２次感染を起こさなかった。

つまり、１次の無症状感染者と接触していた１１名のうち９人は、２次感染を起こさなかった１次の無症状感染者９人のいずれかと接触していた可能性もあるわけです（この２次感染者９人が感染した原因は、別のところからウイルスをもらった可能性もある）。従って、確実に１次の無症状感染者から感染したと言える２次感染者は、１１名－９名＝２人に絞られます。

計算し直すと、この場合の無症状感染率は、

２／２９９×１００≒０．７％

となります。

ただし、繰り返しになりますが、そもそもこの論文に無症状感染率を求めるのは間違いですから、意味のない数字ですね。

（ゆーな2357さん、伊賀治さん、ご指摘ありがとうございました）